Apesar de ter realizado alguns avanços na área da óptica e de estes trabalhos não perderem qualquer crédito, a verdade é que a grande paixão de Kepler era o céu, e assim, é normal que seja na área da Astronomia que este se destacou e realizou estudos. Por esta razão, desde cedo começou a publicar livros desta área, sendo o primeiro Mysterium Cosmographicum (O Mistério Cosmográfico), em 1596, onde tenta encontrar a base geométrica do Universo, utilizando como base a teoria heliocêntrica de Copérnico.
Em Mysterium Cosmographicum, Kepler teorizou que haveria uma relação entre o número de sólidos Platónicos, que são cinco, e o número de planetas conhecidos na altura, que eram seis: Mercúrio, Vénus, Terra, Marte, Júpiter e Saturno. Na tentativa de explicar a geometria do Universo, Kepler defendeu que cada sólido platónico poderia ser inscrito e circunscrito por superfícies esféricas e que colocando cada sólido dentro de outro por uma ordem específica formar-se-iam seis superfícies esféricas. Colocando as superfícies esféricas a intervalos que correspondiam ao raio orbital relativo de cada planeta, Kepler construiu o seu modelo, correspondendo a superfície esférica exterior a Saturno inscrita por um cubo, dentro do qual está a superfície esférica de Júpiter inscrita por um tetraedro, sucedida por Marte, o dodecaedro, a Terra, o icosaedro, Vénus, o octaedro e a superfície esférica mais interior, que é a de Mercúrio. Utilizando o seu modelo, Kepler foi capaz de ainda calcular a relação entre os períodos orbitais de cada planeta através do raio da sua esfera: começando pela esfera mais interna, o aumento no período orbital será igual ao dobro da diferença entre o raio de duas esferas, ou seja, se a diferença entre o raio da esfera relativa a Mercúrio e a esfera relativa a Vénus fosse 2, então o período orbital de Vénus será 4 vezes maior do que o de Mercúrio. Apesar de grande parte do seu modelo se encontrar dentro dos limites da precisão das medições astronómicas da altura, Kepler desistiu desta forma de calcular o período orbital pois considerava-a demasiado inexacta. Em 1621 viria a ser publicada uma segunda edição de Mysterium Cosmographicum contendo vários acertos aos cálculos e melhorias às afirmações realizadas 25 anos atrás, assim como métodos de cálculo da excentricidade das órbitas planetárias que levariam a um modelo de esferas e sólidos platónicos mais exacto.
O aparecimento de uma nova estrela em 1604 ganhou o interesse de Kepler, que começou a executar observações sistemáticas desta que duraram 17 meses, culminando num livro publicado dois anos depois com o título De Stella Nova. O conjunto de observações feitas por Kepler veio reforçar a ideia de que os céus não eram imutáveis, ao contrário da noção aceite até então, fruto do pensamento grego da altura de Aristóteles e nunca refutado por pressões da Igreja, que não podia aceitar que os céus não eram perfeitos e imutáveis.
Com a morte de Tycho Brahe, Kepler herda duas peças importantes para o seu sucesso como astrónomo: as observações das posições de Marte feitas quase diariamente ao longe de 30 anos por Tycho e o seu posto como matemático imperial em Praga. Com as observações de Tycho, Kepler teve acesso a milhares de apontamentos exactos que lhe permitiram analisar o movimento celeste de Marte e com o seu posto teve acesso a tempo livre e dinheiro para o fazer.
Após anos a analisar a quantidade imensa de informação deixada por Brahe, Kepler formula duas das três leis do movimento planetário pelas quais ficaria bastante conhecido, publicando-as no livro Astronomia nova. Neste livro, Kepler apresenta ao leitor todo o processo intelectual que o leva à conclusão final. Ao estudar os modelos geométricos para o movimento planetário existentes (o de Ptolomeu, o de Copérnico e o de Tycho Brahe), Kepler afirma que apenas tendo como base observações, os três são indistinguíveis, prevendo aproximadamente as mesmas posições dos planetas mas falhando na previsão das posições dos mesmos no futuro. De seguida prova que as medições efectuadas por Tycho não contêm nenhum erro e que não se enquadram em nenhum dos modelos até então aceites, sendo necessária a criação de um novo modelo geométrico do movimento celeste. Desta necessidade surgem as duas leis já referidas. São elas:1ª - “ As órbitas dos planetas são elipses com o Sol num dos focos.”
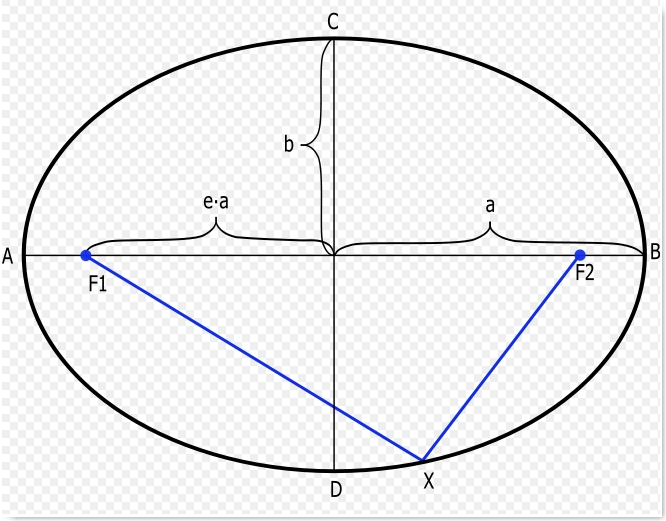
Uma elipse é uma das quatro secções cónicas, e apresenta dois focos, sendo a excentricidade de uma elipse tanto maior quanto maior a distância entre os dois focos. Ao analisar as observações referentes a Marte, Kepler conclui que uma órbita circular nunca se ajustaria às posições observadas, teorizando que a órbita teria uma forma mais oval, acabando por descobrir que uma elipse se ajustaria às observações realizadas. As órbitas dos planetas do Sistema Solar apresentam excentricidades muito reduzidas, ou seja, a distância entre os dois focos é reduzida (em distâncias astronómicas).
2ª - “Em intervalos de tempo iguais, a área varrida pelo segmento de recta que liga o planeta ao Sol é sempre igual.”
A segunda lei de Kepler aparece, na verdade, em primeiro lugar no seu livro, como resultado da constatação de que a velocidade de um planeta é inversamente proporcional à distância do mesmo ao Sol, permitindo-lhe esta conclusão calcular a posição do planeta através da área “varrida” pelo segmento de recta ligando o planeta ao Sol. Apesar de lhe permitir calcular a posição do planeta em questão em intervalos de tempo, esta forma de calcular a posição orbital apresentava um grande problema que era o facto de não permitir calcular a posição de um planeta em cada momento exacto. Este problema iria mais tarde ser resolvido através do desenvolvimento do Cálculo.
A terceira lei de Kepler apenas seria publicada 10 anos depois da publicação de Astronomia Nova, em 1619 com a publicação de Harmonices Mundi (A Harmonia do Mundo):
3ª - “O quadrado do período de revolução é directamente proporcional ao cubo do semi-eixo maior da órbita.”
Esta lei traduz-se numa equação: (T^2)= k.(R^3) em que k é uma constante de proporcionalidade. O estudo desta equação permitiu comprovar que ela pode ser aplicada em qualquer sistema celeste sendo o kconstante para todo o sistema, desde que o astro central assumido fosse o mesmo para todos os corpos. Isto quer dizer que, no caso do Sistema Solar, considerando o Sol como astro central, a constante será a mesma para todos os planetas que orbitam em torno deste (por exemplo a Terra, Marte ou Saturno) enquanto que se assumirmos Júpiter como astro central em relação às suas luas, apesar da constante ser diferente à do sistema com o Sol como astro centra, a relação de proporcionalidade manter-se-á igual para todos os corpos a orbitar em torno de Júpiter.
Neste livro, Kepler procura encontrar, tal como o título indica, a harmonia existente no mundo e no universo, ou seja, a relação matemática e melódica entre o que nos rodeia. O livro foca-se em cinco áreas: os polígonos regulares, a congruência de figuras, a origem da proporção harmónica na música, as configurações harmónicas na astrologia e a harmonia do movimento dos planetas. É impressionante o modo como através dos seus cálculos Kepler apresenta uma relação entre a velocidade angular máxima e mínima de cada planeta encontrando para quase todos um equivalente musical para a variação destas velocidade, ou seja, no caso da Terra, ele descobre que a variação entre as duas velocidades é de 16/15 traduzindo-se esta relação num semi-tom.
Perto da sua morte, em 1623, Kepler termina o seu último e mais trabalhoso livro, considerado por muitos a sua maior obra, Tabulae Rudolphinae, que apenas viria a ser publicado 3 anos antes da sua morte, em 1627. Este livro é um catálogo das estrelas e planetas, onde Kepler compila toda a informação recolhida por Tycho numa série de tabelas e mapas celestes extremamente correctos que permitiam prever a posição dos planetas no céu. Contendo informação sobre a posição de mais de 1400 estrelas, exemplos de como calcular a posição dos planetas no Sistema Solar, assim como explicações para corrigir erros provocados pela refracção atmosférica, é normal que este tenha sido considerado o maior trabalho de Kepler.
Sem comentários:
Enviar um comentário