Com o florescimento das ciências e da busca do saber proporcionado pelo sistema educativo grego, os cientistas começaram a rejeitar a busca do sobrenatural como explicação para os mais variados fenómenos, sendo feitas, nesta época, descobertas bastantes interessantes, por exemplo, nos ramos da matemática, biologia e, claro, da física.

Por volta do século III a.C., a Grécia, assim como grande parte dos países mediterrânicos, são conquistados por Roma cujos objectivos não se encontravam direccionados para a busca de uma maior compreensão do universo ou do mundo natural, assistindo-se, assim, a um desenvolvimento de ciências e invenções com aplicações mais práticas, como as famosas estradas romanas ou o seu formidável poder militar. A assimilação da Grécia pelo Império Romano também levou a que se perdessem uma grande parte dos textos escritos pelos cientistas e filósofos gregos, levando isto a que apenas aqueles que preservaram a língua grega fossem capazes de aceder ao pouco conhecimento que foi salvo.
Estes dois factores vão ser cruciais na história da ciência ocidental.

No século V assistimos àquilo a que se pode chamar "o destino dos grandes impérios". O império romano encontra-se em declínio e é destruído, perdendo-se o pouco do conhecimento grego que perdurara.
Com a queda do império romano, dá-se início à Idade Média. Chamada por muitos cientistas a Idade das Trevas, nesta época, que perdura até ao Renascimento, a razão volta-se para a fé e o temor a Deus. A Europa transforma-se: os pensadores cristãos apercebem-se da necessidade de aprofundar a fé, e, assim, assistimos a um aumento da devoção, assume-se um sistema monárquico nos vários países criados após a queda de Roma e a igreja católica começa a ganhar poder. Como todos sabemos, a ascensão da igreja católica na hierarquia do poder sobre a Europa levou a um bloqueio ao avanço tecnológico.
Neste período da história, apesar de alguns especialistas afirmarem que houve o início de várias descobertas que se realizaram durante o Renascimento, a verdade é que poucos são os avanços tecnológicos e científicos feitos. Assim, a Idade Média corresponde a um período de aproximadamente 1000 anos em que poucos são os avanços tecnológicos feitos. Esta é a razão pela qual a Idade Média é conhecida como a Idade das Trevas.

Nos finais do século XIII ou XIV, assistimos ao nascimento de uma novo período da História: o Renascimento. Inspirado nas referências da antiguidade, este período é marcado pela sua evolução tecnológica, social, económica e cultural. Apesar de pressionados pela Igreja, os cientistas e pensadores europeus fomentam uma visão em que deixam de se dedicar à devoção (Deus no centro do mundo) e focam-se no Homem (Homem no centro do mundo), criando-se uma busca pelo conhecimento de tudo o que rodeia o Homem: o espaço, a Natureza e o próprio Homem.

Assistimos, finalmente, ao florescimento do conhecimento e da busca pelo desconhecido. É neste fervilhar de ideias e teorias que nascem cientistas como Galileu, Copérnico, Kepler e Newton, sendo muitos deles perseguidos pela Inquisição graças às suas ideias e teorias "hereges", que mais tarde se provariam correctas.
É também nesta época que vemos surgir o processo experimental tal como o conhecemos hoje, onde há a elaboração de uma teoria, de uma experiência com fim a provar essa teoria e uma prova ou refutação dessa teoria pela verificação ou não da verdade através da experiência.
No ramo da Física vemos aparecer o telescópio de Galileu, a Teoria da Gravitação Universal e as três leis de Newton, o modelo heliocêntrico de Copérnico e as leis de Kepler, entre tantos outros avanços magníficos.
A partir desta época, o conhecimento e o desenvolvimento tecnológico têm-se vindo a dar de modo constante até à chamada "Era dos Computadores" em que há quem diga que foi possível, graças a eles, descobrir mais em 50 anos do que nos 100 ou 300 anos anteriores.
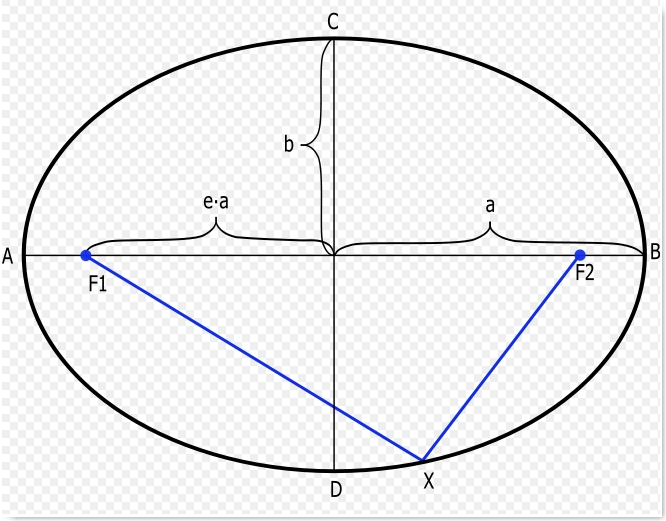
 Após anos a analisar a quantidade imensa de informação deixada por Brahe, Kepler formula duas das três leis do movimento planetário pelas quais ficaria bastante conhecido, publicando-as no livro Astronomia nova. Neste livro, Kepler apresenta ao leitor todo o processo intelectual que o leva à conclusão final. Ao estudar os modelos geométricos para o movimento planetário existentes (o de Ptolomeu, o de Copérnico e o de Tycho Brahe), Kepler afirma que apenas tendo como base observações, os três são indistinguíveis, prevendo aproximadamente as mesmas posições dos planetas mas falhando na previsão das posições dos mesmos no futuro. De seguida prova que as medições efectuadas por Tycho não contêm nenhum erro e que não se enquadram em nenhum dos modelos até então aceites, sendo necessária a criação de um novo modelo geométrico do movimento celeste. Desta necessidade surgem as duas leis já referidas. São elas:
Após anos a analisar a quantidade imensa de informação deixada por Brahe, Kepler formula duas das três leis do movimento planetário pelas quais ficaria bastante conhecido, publicando-as no livro Astronomia nova. Neste livro, Kepler apresenta ao leitor todo o processo intelectual que o leva à conclusão final. Ao estudar os modelos geométricos para o movimento planetário existentes (o de Ptolomeu, o de Copérnico e o de Tycho Brahe), Kepler afirma que apenas tendo como base observações, os três são indistinguíveis, prevendo aproximadamente as mesmas posições dos planetas mas falhando na previsão das posições dos mesmos no futuro. De seguida prova que as medições efectuadas por Tycho não contêm nenhum erro e que não se enquadram em nenhum dos modelos até então aceites, sendo necessária a criação de um novo modelo geométrico do movimento celeste. Desta necessidade surgem as duas leis já referidas. São elas:





















 No seu trabalho Galileu revelou este mesmo tipo de análise. O movimento mais elementar, dizia ele, é uniforme. Segue-se o movimento acelerado, que então já pode ser uniformemente acelerado ou não uniforme. Galileu escolheu o mais simples e explorou então se a aceleração é uniforme quanto ao tempo ou à distância.
No seu trabalho Galileu revelou este mesmo tipo de análise. O movimento mais elementar, dizia ele, é uniforme. Segue-se o movimento acelerado, que então já pode ser uniformemente acelerado ou não uniforme. Galileu escolheu o mais simples e explorou então se a aceleração é uniforme quanto ao tempo ou à distância.



 Isto acerca-se muito do teorema empregado por Galileu para demonstrar a sua própria lei, confrontando distância e tempo no movimento acelerado.
Isto acerca-se muito do teorema empregado por Galileu para demonstrar a sua própria lei, confrontando distância e tempo no movimento acelerado. 



